Hiểu về thuật toán QuickSort

Thuật toán dựa trên kỹ thuật chia để trị,được đề xuất bởi C.A.R Hoare
Ý tưởng như sau:

Sắp xếp dãy khóa k[1..n] thì có thể coi là sắp xếp đoạn từ chỉ số 1 tới chỉ số n trong dãy khóa đó.
Nếu đoạn đó có ít hơn 2 khóa thì không cần làm gì cả, nếu đoạn đó có ít nhất 2 khóa, ta chọn một khóa ngẫu nhiên nào đó làm chốt (pivot). Mọi khóa nhỏ hơn khóa chốt được xếp vào vị trí đứng trước chốt,mọi khóa lớn hơn chốt được xếp vào vị trí sau chốt.Sau phép hoán chuyển như vậy thì đoạn đang xét được chia làm 2 đoạn khác rỗng mà mọi khóa trong đoạn đầu đều <= chốt và mọi khóa trong đoạn sau đều >= chốt. Vấn đề trở thành sắp xếp 2 đoạn mới được tạo ra (độ dài ngắn hơn độ dài đoạn ban đầu) bằng phương pháp tương tự (gọi đệ quy)
Độ phức tạp là O(n*lgn)

#include<stdio.h>
#include<stdlib.h>
#defineMAX 10000
char*input="day_so.inp";
floata[MAX];
intN;

void quick_sort(intl,intr)
     {
                    floattg;
                    floatpivot;
                    inti,j;
                    if(l<r)                //Trường hợp suy biến
                      {
                            i=l;j=r;
                            pivot=a[random(r-l+1)+l];    //Các bạn đặc biệt chú ý chỗ này 
                            do
                                  {
                                       while(a[i]<pivot) i++;
                                       while(a[j]>pivot) j--;
                                       if(i<=j)   
                                          {
                                               tg=a[i];
                                               a[i]=a[j];
                                               a[j]=tg;
                                               i++;j--;
                                          }
                                  }
                            while(i<=j);
                            quick_sort(l,j);
                            quick_sort(i,r);
                       }
     }
                    
                     
void main()
    {
          FILE *f;
          inti;
          /* Đọc dữ liệu từ FILE */    
          f=fopen(input,"r");
                    fscanf(f,"%d",&N);                    
                    for(i=0;i<N;i++) 
                    fscanf(f,"%f",&a[i]);
          fclose(f);
          quick_sort(0,N-1);
      /* In ra kết quả */
      printf("\n Mang sau khi da sap xep la:\n");   
          for(i=0;i<=N-1;i++)   printf("%f\n",a[i]);
          getch();

    }

Các bạn lưu ý trong đoạn code của mình dùng “pivot=a[random(r-l+1)+l]”,cái này rất nhiều sách không đề cập tới,thông thường người ta chọn chốt là phần tử đầu dãy a[l] hoặc cuối dãy a[r]
nhưng với bộ dữ liệu đặc biệt sẽ làm tăng thời gian thực hiện chương trình, do đó mình chọn phần tử bất kì làm chốt.

Phép chọn pivot cần có độ phức tạp O(1).

Pivot tối ưu là trung vị (median) của mảng, tức là một giá trị sao cho một nửa số phần tử của mảng nhỏ hơn nó và nửa còn lại lớn hơn hoặc bằng nó. Nhưng bởi vì không có cách nào O(1) để tính được trung vị, người ta chỉ có thể chọn pivot một cách ngẫu nhiên và bất kể cách đó ngẫu nhiên thế nào thì độ phức tạp của Quicksort trong trường hợp xấu nhất vẫn là O(n^2), không thể giảm được nữa.

Do đó để giảm thời gian tính toán, nên chọn pivot theo những công thức rất đơn giản (chẳng hạn như lấy phần tử đầu tiên của mảng, lấy trung bình cộng của phần tử đầu tiên và cuối cùng trong mảng, hoặc lấy trung bình cộng của 4 phần tử trong mảng), không nên dùng công thức phức tạp nhất là công thức chứa lời gọi hàm (random,…) thì càng không nên.

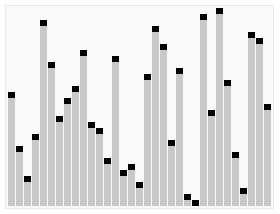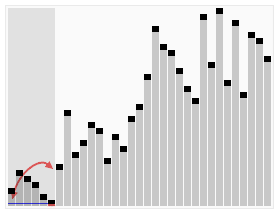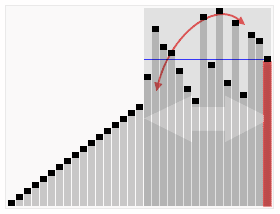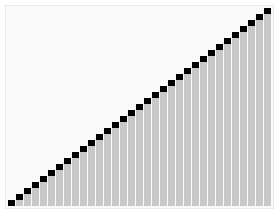
Dưới đây là mô phỏng về thuật toán giúp bạn hiểu hơn nhé